
Tutorial on Introduction to biostatistics
Statistical Distributions
Statistical distributions are classified into two categories - discrete and continuous.
Discrete distributions
Binomial distribution
It describes the possible number of times that a particular event will occur in a sequence of observations. The event is coded in binary fashion; it may or may not occur. The binomial distribution is used when a researcher is interested in the occurrence of an event, not in its magnitude. For instance, in a clinical trial, a patient may survive or die. The researcher studies only the number of survivors, not how long the patient survives after treatment.
Poisson distribution
The Poisson distribution is an appropriate model for count data. Examples of such data are mortality of infants in a city, the number of misprints in a book, the number of bacteria on a plate, and the number of activations of a Geiger counter.
Continuous distributions
Normal distribution
The normal distribution (also called a Gaussian distribution) is a symmetric,
bell-shaped distribution with a single peak. Its peak corresponds to the mean, median, and mode of the distribution.
Normal distribution is characterized by two numbers. Mean gives the location of the peak, and the standard deviation gives the width of the peak.
A data set that satisfies the following four criteria is likely to have a nearly normal distribution:
1. Most data values are clustered near the mean, giving the distribution a well-defined single peak.
2. Data values are spread evenly around the mean, making the distribution symmetric.
3. Larger deviations from the mean become increasingly rare, producing the tapering tails of the distribution.
4. Individual data values result from a combination of many different factors, such as genetic and environmental factors.
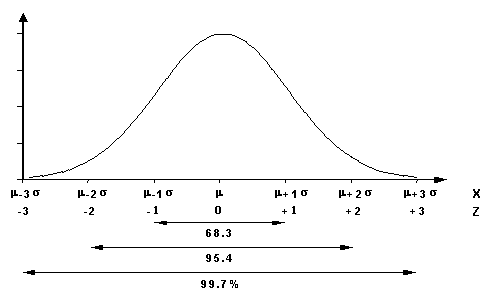
The 68-95-99.7 Rules for a Normal Distribution:
* About 68.3% of the data in a normally Distributed data set will fall within
1 standard deviation of the mean.
* About 95.4% of the data in a normally distributed data set will fall within
2 standard deviations of the mean.
* About 99.7% of the data in a normally distributed data set will fall within
3 standard deviations of the mean.